Энергии вихревого движения жидкости и возможности её практического использования

В настоящее время во всем мире активно ведется поиск новых альтернативных источников энергии, не наносящих вреда окружающему пространству. В процессе этого поиска сформировались два основных направления получения такой энергии.

     Основоположником первого направления считается Н.Тесла, с его идеей получения энергии из окружающего пространства.  О его идеях, в частности запатентованных им трансформаторе, двигателе на постоянных магнитах и т.д. ведется активная дискуссия.

        Основоположником второго направления по праву считается В.Шаубергер с разработанной им теорией энергии воды. Многие авторы пишут о безрезультатных попытках использовать на практике теорию В.Шаубергера , а также изготовить вихревой двигатель.

        Один из сайтов, посвящённый вопросам исследования вихревой энергии, выбрал своим эпиграфом цитату «ЭНЕРГИЯ ПЕРВИЧНА - ЭТО ПРИЧИНА, ФОРМА ВТОРИЧНА - ЭТО СЛЕДСТВИЕ». Этим подчеркивается то, что человечеству пока не ясен основополагающий принцип, объясняющий процессы, протекающие в вихревых аппаратах.

        В предлагаемой статье мы хотим предложить к рассмотрению  вопросы практического применения вихревого движения жидкости.

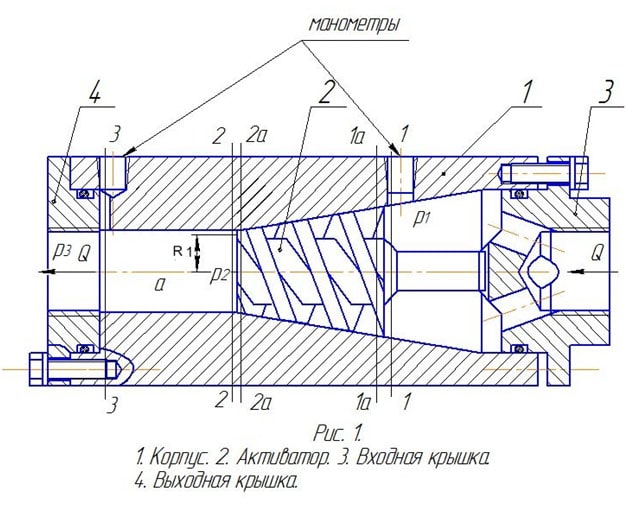
        Для объяснения механизма образования дополнительной энергии в аппаратах, реализующих вихревое движение жидкости, рассмотрим устройство, схема которого приведена на рис.1 и назовем его гидроциклон (Г.Ц.)

        Гидроциклон состоит из корпуса 1 с коническим центральным каналом, в котором расположен активатор, выполненный в виде конуса, на образующей которого расположен сужающийся винтовой канал  и двух крышек - входной 3 и выходной 4. (Рис.1)

       Допустим, что через Г.Ц. проходит  жидкость с расходом Q.

       Рассмотрим уравнение энергии для сечений 2а-2а  активатора, -  на выходе из сужающегося винтового канала и 2-2 - на входе в канал (а) (Рис.1).  Давление в этих сечениях одинаковое и равно р₂. В сечении 2а-2а поток движется по винтовому каналу плоскопараллельно, и энергия единицы массы потока W_2a определяется из выражения:

                                                                        W_2a=E_o + p_2 ⁄ ρ + Q^₂ ⁄ 2f²'

 где:  E_o- внутренняя энергия единицы массы потока,

          f - площадь поперечного сечения сужающегося винтового канала на выходе из активатора,

          ρ - плотность рабочей жидкости,

          Q - расход  рабочей жидкости.

 В сечении 2-2 поток одновременно движется параллельно оси со скоростью Q ⁄ F₂ (поскольку соблюдается принцип не разрывности потока) и  вращается вокруг оси с угловой скоростью ω=Q ⁄ fR

Энергия единицы массы потока определяется из выражения:

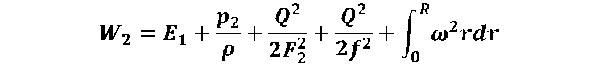
, где E₁- внутренняя энергия единицы массы потока в сечении 2-2,

      F₂- площадь сечения канала (а),

      R - радиус  винтового канала  на конусе активатора (Рис.1),

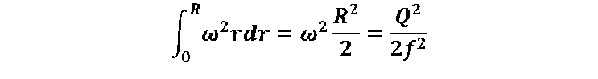
- энергия единицы массы потока, возникшая  от действия центробежных сил переносного вихревого движения. Поскольку приток энергии из вне отсутствует W_2a=W₂.

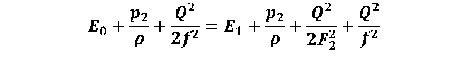       (1)

Указанное уравнение учитывает то, что часть гидравлической энергии потока Q² ⁄ 2f²  при входе в канал (а) перешла во внутреннюю энергию (внезапное расширение потока, т.е. отрыв потока от стенок).

        Учитывая то, что F₂>>f  т.е  Q²⁄ 2F₂² =0, из уравнения (1) следует:

                                               Q²⁄ 2f²=E₀ - E₁,

 т.е., часть внутренней энергии потока переходит в гидравлическую энергию переносного движения, которая на выходе из Г.Ц. переходит в потенциальную энергию давления.

         Рассмотрим уравнение Бернулли для сечений 1-1; 2а-2а; 2-2 и 3-3. Приняв во внимание , что в сечении 3-3 поток имеет плоскопараллельное движение (в случае необходимости в канале (а) может быть установлен выпрямитель потока), получим формулу:

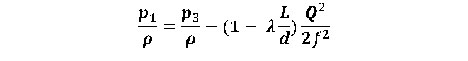           (2) ,

где λ - коэффициент гидравлического сопротивления,

      L - приведенная длинна сужающегося винтового канала,

      d - средний гидравлический диаметр поперечных сечений сужающегося винтового канала,

     p₁- давление на входе в Г.Ц.,

     p₃- давление на выходе.

Следует учесть, что это выражение верно при отсутствии кавитации, т.е. при р₂>0 или p₃>Q²⁄ f² (давление абсолютное).

       Из уравнения (2) видно, что мощность потока на выходе из Г.Ц. больше чем на входе в него за счет части внутренней энергии рабочей жидкости, причем величина этой разности определяется геометрическими размерами активатора L; d; f и величиной расхода рабочей среды. Разница  между входной и выходной гидравлической мощностью δN.

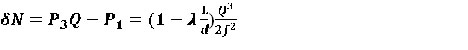
 δN зависит от Q и от f и может достигать практически любых величин.

        По описанному выше принципу работают сопла и имплозионная машина(в том числе и «домашний генератор») Шаубергера, вихревой двигатель Клема, тепловые генераторы Потапова.

        Наша творческая группа занимается изучением данного направления уже более 10 лет. За это время нами разработан метод расчета турбин на выше приведенном принципе для любой мощности и сделана конструктивная проработка турбины мощностью 20 Квт, экспериментальные образцы подвесных лодочных моторов (водометов) тяговым усилием 20 и 50 кг, работающие на забортной воде.

        Кроме того, нами разработаны аппараты, реализующие самовоспроизводящийся вихрь, разработана методика их расчета и на этом принципе проработаны:

       1. Отопительный котел тепловой производительностью 45 Квт;

       2.Двигатель мощностью 2,7...4,5 Квт.

          Работы по практическому использованию энергии вихревого движения жидкости до настоящего времени нами проводились как поисковые, основанные  исключительно на собственном энтузиазме. Но, накопленный опыт позволяет осуществить выход на изготовление опытных образцов. Наша группа ищет инвестора, готового на взаимовыгодных условиях, финансировать проведение дальнейшей работы, изготовления образцов оборудования, проведения их испытаний.

        В случаи интереса к данной информации просьба писать:

       E-mail: yushtexcenter@yandex.ru